Some sample groups

Consider a line with labeled ends. There are two things we can do to it while leaving the line in place. We can "do nothing" (think of adding zero to a number) and we can flip the line. (Or rotate it 180 degrees, with the same effect.) We can combine these operations, although the only interesting combination is flipping the line twice, which gives us the original figure. We can make a multiplication table of the operations:

	do nothing	flip
do nothing	original	flipped
flip	flipped	original

or

	I	s
I	I	s
s	s	I

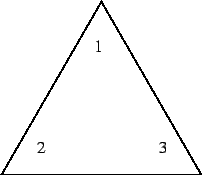
Not very exciting. But consider an equilateral triangle cutout, pinned to some cardboard, so you can rotate it. There are two other positions leaving the triangle in place, corresponding to rotations of 120 and 240 degrees.

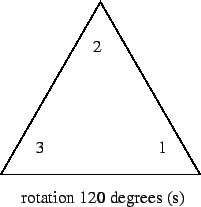
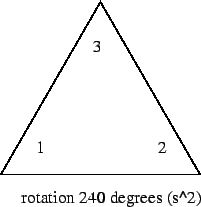
If we call the rotations s and s² and "do nothing" I we can make the following table, whose values the reader should be able to verify:

	I	s	s2
I	I	s	s2
s	s	s2	I
s2	s2	I	s

Similarly we can make regular polygons with any number of sides, and consider their rotations, keeping the outline of the figure constant. We can also extend the idea to a circle with a mark somewhere on it; there are infinitely many rotations in this case, giving us a group with an (uncountable) infinite number of members. These groups are called cyclic, or Cyc_n¹ where _n is the number of sides. So our first group is Cyc₂, the triangle Cyc₃, the square Cyc₄, and so on.

The next step is to take the polygons, in our case the triangle, off the cardboard. Now we can not only rotate them, but we can flip them around an axis, giving us three new states (and operations to generate the states.)

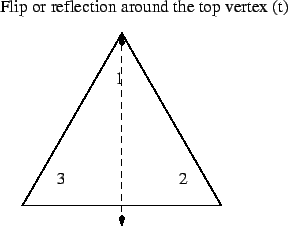
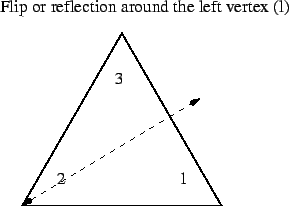
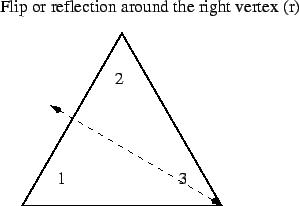
And we get an expanded multiplication table:

	I	s	s2	t	l	r
I	I	s	s2	t	l	r
s	s	s2	I	r	t	l
s2	s2	I	s	l	r	t
t	t	l	r	I	s	s2
l	l	r	t	s2	I	s
r	r	t	l	s	s2	I

Notice something different here: s followed by t gives r, but tfollowed by s is l. Unlike the previous groups, or the arithmetic we learn as children, the rotations and reflections of the triangle, simple though this group is, are not commutative. Some elements (s, s²) commute with each other, but only the identity element I commutes (trivially) with everything in the group. Also note that while we defined all three flips of the triangle, in a real sense we only need one. We started out being able to rotate the triangle; given the ability to flip it on its back, we can keep on rotating, and reach all of the configurations of the other flips. As illustration here's a table where l has been replaced by ts and r by st.

	I	s	s2	t	ts	st
I	I	s	s2	t	ts	st
s	s	s2	I	st	t	ts
s2	s2	I	s	ts	st	t
t	t	ts	st	I	s	s2
ts	ts	st	t	s2	I	s
st	st	t	ts	s	s2	I

For comparsion, look at the table for Cyc₆, the rotations of the hexagon (chosen for having the same number of elements):

	I	s	s2	s3	s4	s5
I	I	s	s2	s3	s4	s5
s	s	s2	s3	s4	s5	I
s2	s2	s3	s4	s5	I	s
s3	s3	s4	s5	I	s	s2
s4	s4	s5	I	s	s2	s3
s5	s5	I	s	s2	s3	s4

If you flip this table (or those of the other Cyc groups) around a diagonal from the top left to the bottom right, you get the same table, which is not the full table of the triangle.

Just as we can look at the rotations of any polygon, we can look at the rotations+flips of any polygon. This class of groups is known as dihedral ("two-faced") groups, or Dih_n,² and the full group of the triangle is Dih₃.

There's something else we can learn from the triangle. Look at the sequence of numbers of each triangle figure, starting from the top vertex and going counterclockwise. The first three, the members of Cyc₃, give (1,2,3), (2,3,1), and (3,1,2) - (1,2,3) on a cyclic conveyor belt. The other three give us (1,3,2), (3,2,1) and (2,1,3). Together the six sequences form all the possible permutations of three elements. This is actually a coincidence, given how we defined the group; in general Dih_n has 2n elements - nrotations and n flips - while permutations have n! n! elements. But the permutations of n elements do in fact constitute a group Perm_n,³ and it just happens that Perm₃ equals Dih₃.