Commutators

The commutator of two group elements a and b is the group element c such that ab = bac. It can be thought of as that element which allows a and b to commute. It may also be defined as Comm(a,b) = a^-1b^-1ab; it should be easy to see that this satisfies the role of c. It should also be clear from both definitions that if a and b commute then c is I, and Comm(a,b) will come out to be I. If the group is abelian so that all pairs a,b commute then the only commutator is I and the commutator subgroup is I. The reverse is also true.

Commutators are preserved by homomorphisms.

$$\phi(a^{-1}b^{-1}ab) = \phi(a^{-1})\phi(b^{-1})\phi(a)\phi(b)$$

and remembering that homomorphisms map inverses to inverses we find

$$\phi(a)^{-1}\phi(b)^{-1}\phi(a)\phi(b)$$

which is a commutator. So if the commutators and their products form a proper subgroup of the group, all endomorphisms will preserve this subgroup, and so it is fully invariant, characteristic, and normal.

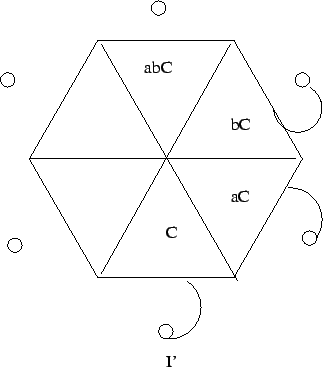
The factor group of commutator subgroups is always abelian. It may help to recall what the factor group is, namely where a normal subgroup is mapped to the identity of some group and its cosets are mapped to the other elements of that group. So multiplication in the factor group can be thought of as membership in cosets of the starting group. If N is a normal subgroup of G, aN is in one coset and bN is in another, then in general aNbN goes to one coset of G, and bNaN may go to yet another. But not when N=C.

For multiplication of cosets to be commutative we need ab and ba to go to the same coset, abC = baC, or in terms of concrete elements abc₁ = bac₂. But we can take c₁ to be I and get ab = bac, which is exactly the definition of commutators! If that was too fast there is a longer derivation: aCbC = abCC = abC = baCC = bCaC.

A third albeit currently less rigorous way of looking at it is that in making the factor group we have gathered up all the commutators of G into C and then mapped them all to I. For the factor group to not be abelian one of the other elements of G/C must be a commutator (if the only commutator is I the group is abelian). But the pre-image of this commutator cannot be a commutator or product of commutators in G, because those have all be mapped to I. Since homomorphism preserves group structure one might suspect this might not be the case. In a sense we have gathered all the non-commutativity of G into a bag and then squished the bag.